Difference between revisions of "Kaustubh Shivdikar"
m (MaxK GNN added) (Tag: Visual edit) |
m (New lines added) (Tag: Visual edit) |
||
| Line 103: | Line 103: | ||
[[File:MaxK teaser.png|right|frameless|109x109px]] | [[File:MaxK teaser.png|right|frameless|109x109px]] | ||
| − | ====== MaxK-GNN: Towards Theoretical Speed Limits for Accelerating Graph Neural Networks Training ====== | + | ======MaxK-GNN: Towards Theoretical Speed Limits for Accelerating Graph Neural Networks Training====== |
{{Nutshell|Presented MaxK non-linearity as a universal approximator to speedup GNN training|title=Paper}} | {{Nutshell|Presented MaxK non-linearity as a universal approximator to speedup GNN training|title=Paper}} | ||
Revision as of 16:02, 7 November 2023
Hi, I am Kaustubh, a Ph.D. candidate studying computer engineering in NUCAR lab at Northeastern University with my advisor David Kaeli. My research focuses on designing hardware accelerators for sparse graph workloads.
My expertise lies in:
- Computer Architecture Simulator Design
- Graph Neural Network Accelerators
- Sparse Matrix Accelerators
- Homomorphic Encryption Accelerators
- GPU Kernel Design
Contact:
- shivdikar.k [at] northeastern [dot] edu
- mail [at] kaustubh [dot] us
Education
- PhD - Computer Engineering, Northeastern University [Expected Fall 2023]
- MS - Electrical and Computer Engineering, Northeastern University [May 2021]
- BS - Electrical Engineering, Veermata Jijabai Technological Institute [May 2016]
Work
- Summer-Fall 2020 Coop: Parallel Computing Lab @ Intel Labs with Fabrizio Petrini.
- Summer-Fall 2019 Coop: Parallel Computing Lab @ Intel Labs with Fabrizio Petrini.
- Summer-Fall 2018 Coop: Mobile Robotics @ Omron Adept with George Paul.
Recent News
- Sept 2023: Served on the HPCA 2024 Program Reviewer's Committee
- Feb 2023: Served on the HPCA 2023 Best Paper Committee
- June 2022: Mentored Lina Adkins for the GNN Acceleration project at REU-Pathways program
- May 2022: Served as Submission chair for HPCA 2023 conference.
- Jan 2020: Taught the GPU Programming Course at NEU
- April 2019: Graduate Innovator Award at the RISE 2019 Research Expo for our poster Pi-Tiles
- April 2018: Best Poster Award at the RISE 2018 Research Expo for our poster The Prime Hexagon
- Nov 2018: Mentored the NEU team for Student Cluster Contest at Super Computing Conference 2018
- Nov 2017: Joined the NEU Team for Student Cluster Contest at Super Computing Conference 2017
Publications
MaxK-GNN: Towards Theoretical Speed Limits for Accelerating Graph Neural Networks Training
Paper in a nutshell: Presented MaxK non-linearity as a universal approximator to speedup GNN training |
(ASPLOS 2024) [PDF] [RG]
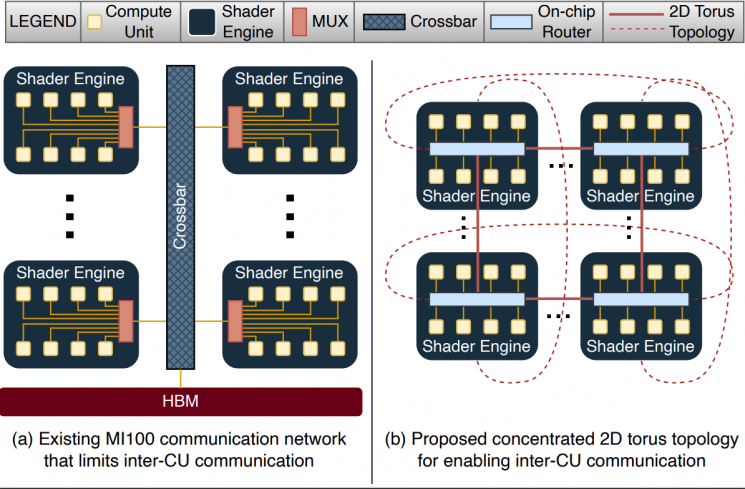
GME: GPU-based Microarchitectural Extensions to Accelerate Homomorphic Encryption
GME in a nutshell: Enhanced the AMD MI-100 GPU on-chip network to accelerate Homomorphic Encryption. |
(IEEE/ACM MICRO 2023) [PDF] [RG] [Slides]
| Abstract |
|---|
| Fully Homomorphic Encryption (FHE) enables the processing of encrypted data without decrypting it.
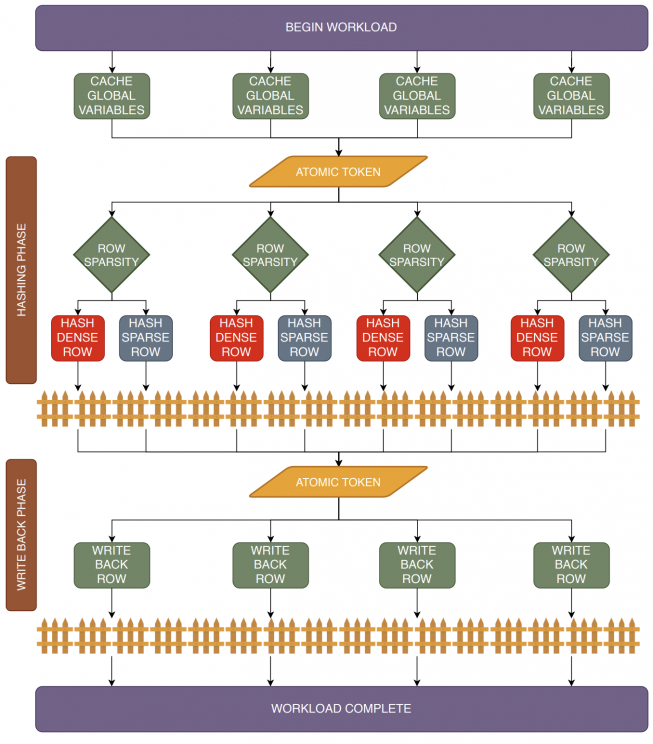
FHE has garnered significant attention over the past decade as it supports secure outsourcing of data processing to remote cloud services. Despite its promise of strong data privacy and security guarantees, FHE introduces a slowdown of up to five orders of magnitude as compared to the same computation using plaintext data. This overhead is presently a major barrier to the commercial adoption of FHE. In this work, we leverage GPUs to accelerate FHE, capitalizing on a well-established GPU ecosystem available in the cloud. We propose GME, which combines three key microarchitectural extensions along with a compile-time optimization to the current AMD CDNA GPU architecture. First, GME integrates a lightweight on-chip compute unit (CU)-side hierarchical interconnect to retain ciphertext in cache across FHE kernels, thus eliminating redundant memory transactions. Second, to tackle compute bottlenecks, GME introduces special MOD-units that provide native custom hardware support for modular reduction operations, one of the most commonly executed sets of operations in FHE. Third, by integrating the MOD-unit with our novel pipelined 64-bit integer arithmetic cores (WMAC-units), GME further accelerates FHE workloads by 19%. Finally, we propose a Locality-Aware Block Scheduler (LABS) that exploits the temporal locality available in FHE primitive blocks. Incorporating these microarchitectural features and compiler optimizations, we create a synergistic approach achieving average speedups of 796x, 14.2x, and 2.3x over Intel Xeon CPU, NVIDIA V100 GPU, and Xilinx FPGA implementations, respectively. |
|
| Authors: Kaustubh Shivdikar, Yuhui Bao, Rashmi Agrawal, Michael Shen, Gilbert Jonatan, Evelio Mora, Alexander Ingare, Neal Livesay, José L. Abellán, John Kim, Ajay Joshi, David Kaeli |
Accelerating Finite Field Arithmetic for Homomorphic Encryption on GPUs
Paper in a nutshell: Optimized modulo "%" operator on NVIDIA V100 GPU to speedup Homomorphic Encryption. |
(IEEE MICRO 2023) [PDF] [RG]
Accelerating Polynomial Multiplication for Homomorphic Encryption on GPUs
Paper in a nutshell: Incorporated NVIDIA V100's shared memory to accelerate Homomorphic Encryption. |
(SEED 2022) [PDF][Slides] [RG]
| Abstract |
|---|
| Homomorphic Encryption (HE) enables users to securely outsource both the storage and computation of sensitive data to untrusted servers. Not only does FHE offer an attractive solution for security in cloud systems, but lattice-based FHE systems are also believed to be resistant to attacks by quantum computers. However, current FHE implementations suffer from prohibitively high latency. For lattice-based FHE to become viable for real-world systems, it is necessary for the key bottlenecks---particularly polynomial multiplication---to be highly efficient.
In this paper, we present a characterization of GPU-based implementations of polynomial multiplication. We begin with a survey of modular reduction techniques and analyze several variants of the widely-used Barrett modular reduction algorithm. We then propose a modular reduction variant optimized for 64-bit integer words on the GPU, obtaining a 1.8x speedup over the existing comparable implementations.
|
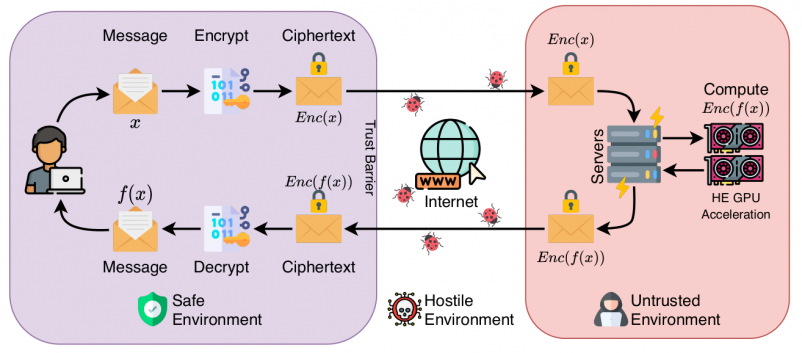
FHE protects against network insecurities in untrusted cloud services, enabling users to securely offload sensitive data |
| Authors: Kaustubh Shivdikar, Gilbert Jonatan, Evelio Mora, Neal Livesay, Rashmi Agrawal, Ajay Joshi, José L. Abellán, John Kim, David Kaeli |
JAXED: Reverse Engineering DNN Architectures Leveraging JIT GEMM Libraries
JAXED in a nutshell: Exposed software cache's vulnerability with a side-channel attack. |
(SEED 2021) [PDF] [Slides] [Poster] [RG]
| Abstract |
|---|
| General matrix multiplication (GEMM) libraries on x86 architectures have recently adopted Just-in-time (JIT) based optimizations to dramatically reduce the execution time of small and medium-sized matrix multiplication. The exploitation of the latest CPU architectural extensions, such as the AVX2 and AVX-512 extensions, are the target for these optimizations. Although JIT compilers can provide impressive speedups to GEMM libraries, they expose a new attack surface through the built-in JIT code caches. These software-based caches allow an adversary to extract sensitive information through carefully designed timing attacks. The attack surface of such libraries has become more prominent due to their widespread integration into popular Machine Learning (ML) frameworks such as PyTorch and Tensorflow.
|
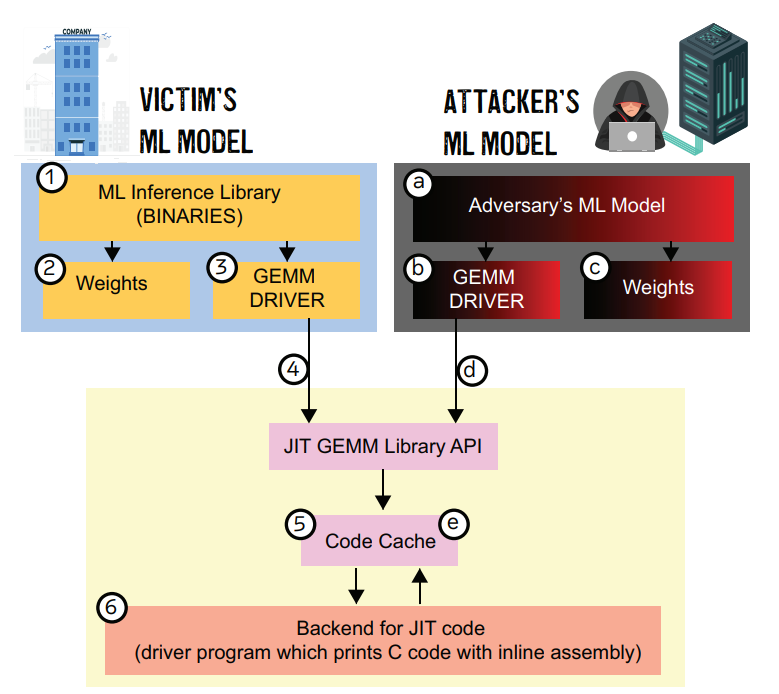
Attack Surface: After the victim’s execution, the victim leaves behind information about its model hyperparameters in the JIT code cache. The attacker probes this JIT code cache through the attacker’s ML model and observes timing information to determine the victim’s model hyperparameters. |
| Authors: Malith Jayaweera, Kaustubh Shivdikar, Yanzhi Wang, David Kaeli |
GNNMark: A benchmark suite to characterize graph neural network training on GPUs
GNNMark in a nutshell: Created a standardized suite of GNN workloads to benchmark GPUs. |
(ISPASS 2021) [PDF] [RG]
| Abstract |
|---|
| Graph Neural Networks (GNNs) have emerged as a promising class of Machine Learning algorithms to train on non-euclidean data. GNNs are widely used in recommender systems, drug discovery, text understanding, and traffic forecasting. Due to the energy efficiency and high-performance capabilities of GPUs, GPUs are a natural choice for accelerating the training of GNNs. Thus, we want to better understand the architectural and system level implications of training GNNs on GPUs. Presently, there is no benchmark suite available designed to study GNN training workloads.
|
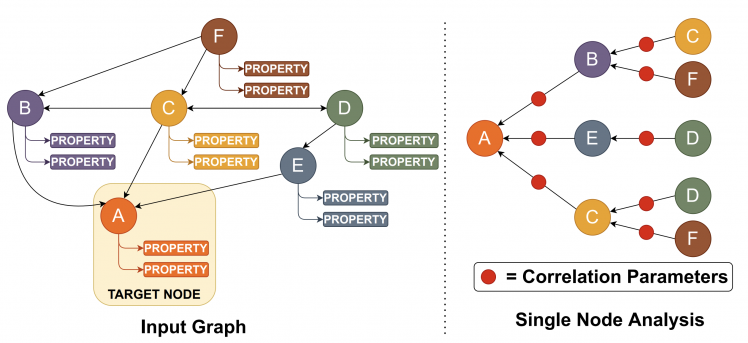
Graph Neural Network Analysis |
| Authors: Trinayan Baruah, Kaustubh Shivdikar, Shi Dong, Yifan Sun, Saiful A Mojumder, Kihoon Jung, José L. Abellán, Yash Ukidave, Ajay Joshi, John Kim, David Kaeli |
SMASH: Sparse Matrix Atomic Scratchpad Hashing
SMASH in a nutshell: Optimized SpGEMM for Intel's PIUMA architecture. |
(MS Thesis, 2021) [PDF] [RG]
Student cluster competition 2018, team northeastern university: Reproducing performance of a multi-physics simulations of the Tsunamigenic 2004 Sumatra Megathrust earthquake on the AMD EPYC 7551 architecture
Paper in a nutshell: Optimizing earthquake simulation workload on AMD CPUs. |
Speeding up DNNs using HPL based Fine-grained Tiling for Distributed Multi-GPU Training
Paper in a nutshell: Evaluating the cluster equipped with NVIDIA GPUs using the Linpack benchmark. |
Video steganography using encrypted payload for satellite communication
Paper in a nutshell: Concealing secret messages in videos. |
(Aerospace Conference 2017) [PDF] [RG]
Missing 'Middle Scenarios' Uncovering Nuanced Conditions in Latin America's Housing Crisis
Paper in a nutshell: Integrating LSTM models with Latin American housing data to devise solutions. |
(Cityscape 2017) [PDF] [RG]
Dynamic power allocation using Stackelberg game in a wireless sensor network
Paper in a nutshell: Employing game theory for power distribution models. |
(Aerospace Conference 2016) [PDF] [RG]
Automatic image annotation using a hybrid engine
Paper in a nutshell: A hybrid engine that merges feature extraction with language models. |
(Indicon 2015) [PDF] [RG]
Posters
- FHE [PDF]
- JAXED [PDF]
- Pi-Tiles (Graduate Innovator Award) [PDF]
- The Prime Hexagon (Best Poster Award) [PDF]
What is KTB Wiki?
KTB Wiki, because the best way to store your knowledge is in an indexed SQL database.
This website was built on KTB Wiki. KTB wiki is my side project/attempt to consolidate knowledge gained during my Ph.D. journey. Though many other platforms provide similar service, the process of creating KTB Wiki was a learning experience since it taught me concepts of indexing, load balancing, and in-memory file systems. KTB Wiki was built using MediaWiki and is intended for research purposes only.
Interesting Reads