Graph Laplacian, (aka Laplace Matrix, Admittance Matrix, Kirchhoff Matrix, Discrete Laplacian, Laplace-Beltrami operator), is simply a matrix representation of a graph.
Laplacian Matrix can be computed as:

Where  is Laplacian Matrix,
is Laplacian Matrix,  is Degree Matrix and
is Degree Matrix and  is Adjacency matrix.
is Adjacency matrix.
| Labelled graph
|
Degree matrix
|
Adjacency matrix
|
Laplacian matrix
|
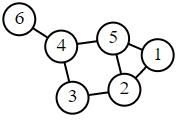
|

|

|

|
Diagonalization of Laplacian
- The Laplacian of an undirected graph is symmetric as well as unitary.
- Using diagonalization:
 (where
(where  is a set of eigenvectors and
is a set of eigenvectors and  is a diagonal matrix containing eigenvalues)
is a diagonal matrix containing eigenvalues)
- Then
 OR
OR 
Normalized Laplacian

Random-walk Laplacian

Keywords
Laplacian Matrix, GNN, Laplace Matrix, Degree Matrix
Warning:
For dynamical systems we consider  largest, but for Laplacian Matrix
largest, but for Laplacian Matrix  is the smallest.
is the smallest.















