Graph isomorphism
-
- Last edited 4 years ago by Kaustubh Shivdikar
-
In graph theory, an isomorphism of graphs (Isomorphic Graphs) G and H is a bijection between the vertex sets of G and H.
Note: In simple terms: Two graphs are isomorphic if they have same graph structure (edges) with the nodes simply renamed (re-labelled).
Such that any two vertices u and v of G are adjacent in G if and only if f(u) and f(v) are adjacent in H.
This kind of bijection is commonly described as "edge-preserving bijection", in accordance with the general notion of isomorphism being a structure-preserving bijection.
Isomorphic graphs are denoted as:
In the case when the bijection is a mapping of a graph onto itself, i.e., when G and H are one and the same graph, the bijection is called an automorphism of G.
The two graphs shown below are isomorphic, despite their different looking drawings.
| Graph G | Graph H | An isomorphism
between G and H |
|---|---|---|
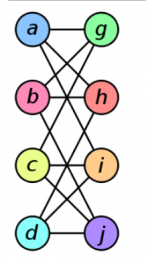
|
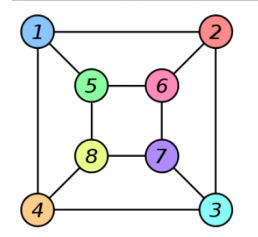
|
|









