Difference between revisions of "Graph Laplacian"
m (Lamda 1 note added) (Tag: Visual edit) |
m (Nutshell added) (Tag: Visual edit) |
||
| Line 1: | Line 1: | ||
| − | Graph Laplacian, (aka Laplace Matrix, Admittance Matrix, Kirchhoff Matrix, Discrete Laplacian, Laplace-Beltrami operator), is simply a '''matrix representation of a graph.''' | + | {{Nutshell|1=Laplacian = Degree Matrix - Adjacency Matrix|title=Graph Laplacian}} |
| + | |||
| + | Graph Laplacian, (aka '''Laplace''' Matrix, '''Admittance''' Matrix, '''Kirchhoff''' Matrix, '''Discrete''' '''Laplacian''', '''Laplace'''-'''Beltrami''' operator), is simply a '''matrix representation of a graph.''' | ||
Laplacian Matrix can be computed as: | Laplacian Matrix can be computed as: | ||
Latest revision as of 17:46, 17 June 2021
Graph Laplacian in a nutshell: Laplacian = Degree Matrix - Adjacency Matrix |
Graph Laplacian, (aka Laplace Matrix, Admittance Matrix, Kirchhoff Matrix, Discrete Laplacian, Laplace-Beltrami operator), is simply a matrix representation of a graph.
Laplacian Matrix can be computed as:
Where is Laplacian Matrix, is Degree Matrix and is Adjacency matrix.
| Labelled graph | Degree matrix | Adjacency matrix | Laplacian matrix |
|---|---|---|---|
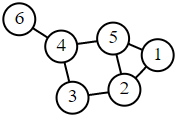
|
Diagonalization of Laplacian
- The Laplacian of an undirected graph is symmetric as well as unitary.
- Using diagonalization: (where is a set of eigenvectors and is a diagonal matrix containing eigenvalues)
- Then OR
Normalized Laplacian
Random-walk Laplacian
Keywords
Laplacian Matrix, GNN, Laplace Matrix, Degree Matrix
Warning: For dynamical systems we consider largest, but for Laplacian Matrix is the smallest.














