You are viewing an old version of this page. Return to the latest version.
Difference between revisions of "Graph Laplacian"
m (Normalized and Random-walk added) (Tag: Visual edit) |
m (Diagonalization added) (Tag: Visual edit) |
||
| Line 40: | Line 40: | ||
|} | |} | ||
| − | == Normalized Laplacian == | + | == Diagonalization of Laplacian == |
| + | |||
| + | * The Laplacian of an undirected graph is symmetric as well as '''[[Matrix Properties|unitary]].''' | ||
| + | * Using [[Eigenvalues and Eigenvectors|diagonalization]]: <math>L = U \Lambda U^{-1}</math> (where <math>U</math> is a set of eigenvectors and <math>\Lambda</math> is a diagonal matrix containing eigenvalues) | ||
| + | * Then <math>U^T = U^{-1}</math> OR <math>UU^T = I</math> | ||
| + | |||
| + | ==Normalized Laplacian== | ||
<math>L_n = D^{-\frac{1}{2}}LD^{-\frac{1}{2}}</math> | <math>L_n = D^{-\frac{1}{2}}LD^{-\frac{1}{2}}</math> | ||
| − | == Random-walk Laplacian == | + | ==Random-walk Laplacian== |
<math>L_{rw} = D^{-1}L</math> | <math>L_{rw} = D^{-1}L</math> | ||
==Keywords== | ==Keywords== | ||
Laplacian Matrix, GNN, Laplace Matrix, Degree Matrix | Laplacian Matrix, GNN, Laplace Matrix, Degree Matrix | ||
Revision as of 03:19, 26 March 2021
Graph Laplacian, (aka Laplace Matrix, Admittance Matrix, Kirchhoff Matrix, Discrete Laplacian, Laplace-Beltrami operator), is simply a matrix representation of a graph.
Laplacian Matrix can be computed as:
Where is Laplacian Matrix, is Degree Matrix and is Adjacency matrix.
| Labelled graph | Degree matrix | Adjacency matrix | Laplacian matrix |
|---|---|---|---|
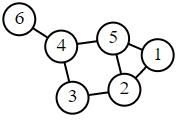
|
Diagonalization of Laplacian
- The Laplacian of an undirected graph is symmetric as well as unitary.
- Using diagonalization: (where is a set of eigenvectors and is a diagonal matrix containing eigenvalues)
- Then OR
Normalized Laplacian
Random-walk Laplacian
Keywords
Laplacian Matrix, GNN, Laplace Matrix, Degree Matrix













